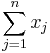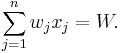Change-making problem

The change-making problem addresses the following question: how can a given amount of money be made with the least number of coins of given denominations? It is a knapsack type problem, and has applications wider than just currency.

1 Mathematical definition
2 Non currency examples
3 Methods of solving
4 See also
5 References

Mathematical definition

Given a set of integer coin values {w₁, w₂, ..., w_n} where w₁ = 1 and w_j < w_j+1 for 1 ≤ j ≤ n − 1, and a positive integer W, find a set of non-negative integers {x₁, x₂, ..., x_n} which minimize

$\sum_{j=1}^n x_j$

subject to

$\sum_{j=1}^n w_j x_j = W.$

Non currency examples

how to make a nine dart finish

Methods of solving

Dynamic programming

Making a list of ways to make each amount from one upwards (an example of a dynamic programming method)

Linear programming

Integer Linear Programming is often a quick way to solve this kind of problem, but the time it will take to resolve the problem is not certain, and may be slow in some cases

Greedy method

In the US (and most other) coin systems, a greedy algorithm of picking the largest denomination of coin which is not greater than the remaining amount to be made will always produce the optimal result. This is not automatically the case, though: if the coin denominations were 1, 3 and 4, then to make 6, the greedy algorithm would choose three coins (4,1,1) whereas the optimal solution is two coins (3,3).

References

J. Shallit. "What this country needs is an 18c piece". Mathematical Intelligencer 25 (2): 20–23. doi:10.1007/BF02984830. http://www.cs.uwaterloo.ca/~shallit/Papers/change2.pdf.
X. Cai (2009). "Canonical Coin Systems for Change-Making Problems". Proceedings of the Ninth International Conference on Hybrid Intelligent Systems: 499–504. arXiv:0809.0400. doi:10.1109/HIS.2009.103.
M. Adamaszek, A. Niewiarowska (2010). "Combinatorics of the change-making problem". European Journal of Combinatorics 31 (1): 47–63. arXiv:0801.0120. doi:10.1016/j.ejc.2009.05.002.